Single Task Choice

Author: Paul Richard McCullough
Published Spring 2011 by Marketing Research Magazine

Download

If you had a choice (no pun intended) between asking respondents 20 choice questions or just one, which approach would you choose?

OK.  Now that you’ve picked 20 because you don’t think one choice task is going to yield a sufficiently accurate model, momentarily assume that, with just one choice task per respondent, you could estimate a disaggregate choice model that had a mean absolute error (MAE) of barely more than one share point and a hit rate of 70 percent or better (that’s really good, if you didn’t already know).  Now which would you choose?  Would you pick the one task approach then?

Why?  Would it be because a shorter interview could increase response rate which, in turn, may improve population representation?  Would you go with the more practical and always popular “saves time and money in field?”  Or because you saved so much interview time, would you combine your choice study with another study – say a brand equity or consumer segmentation or maybe an A&U – and kill two birds with one stone?

How about the possibility of applying choice-based (or ratings-based, for that matter) conjoint to areas heretofore inaccessible to the joys of disaggregate conjoint?  Integrating elaborate conjoint designs into methodologies such as taste tests, laboratory simulations, home use tests, post card studies, in-store intercepts, even mobile device-based choice-based conjoint (CBC) becomes feasible when the number of choice tasks is very small.

Oh, the Possibilities

          Figure 1:  The World As Some See It
Of course, this is crazy, right?  Yes, it would be nice to offer just a single choice task to each respondent and end up with an accurate set of disaggregate utilities.  But that’s just silly.  You can’t estimate a regression model with one case, even if that model only had one predictor and choice models typically have lots and lots.  It’s mathematically impossible.  More parameters than degrees of freedom?  Call the men in the white coats.  Sounds like somebody needs a state-sponsored vacation.  But before you ship me off to the Pink Pill Palace, consider this.

           Figure 2:  The World As Others See It

Back in the day, before hierarchical Bayes, we were forced to estimate aggregate logit models, somewhat curiously called “mother” logit.  We didn’t have enough information to estimate choice models for each respondent, so we pooled their answers and built a model for the entire sample.  And we jumped through lots of algebraic hoops trying to compensate for all that heterogeneity we weren’t capturing. HB does better because it captures some of the heterogeneity that aggregate models miss.  But what if there’s not much heterogeneity to capture?  Does HB still work better?  Well, no, not if the sample is so homogeneous that every respondent has exactly the same preferences.  Then the disaggregate model is no better than the aggregate model.  Whether HB is better than mother logit is directly related to the degree of heterogeneity in the sample.  Little heterogeneity, little improvement.  Lots of heterogeneity, lots of improvement.

What I’m getting to is this:  if I had a sample of extremely homogeneous respondents, I could build a mother logit model and assign the aggregate utilities to each person in the sample.  This “disaggregate” model would work almost as well as an HB-derived model.  If all the respondents were identical in their choice behaviors, the “disaggregate” model would be equivalent to the HB-derived model.  Guaranteed.

If my sample size was big enough, I could give each respondent one choice task and build the same mother logit model that I would get if I gave each respondent 10 choice tasks (or 20).   Of course, I’d give each respondent a different choice task but, still, just one choice task each.  As long as the sample was sufficiently homogeneous, I get the same answer with one task, 10 tasks, 20 tasks and/or hierarchical Bayes.

A Tale of Two Camels

OK.  We’re still not all the way there.  But we’re getting closer.  You might correctly point out that one rarely, if ever, has a homogeneous sample and, therefore, this approach is useless.  But you must admit that if we could identify a tightly homogeneous group of people of sufficient sample size, we could build an accurate, “disaggregate” choice model using just one task per person.  Now hold that thought.

I like to think the world can be divided in to two types of people: those that think there are naturally occurring segments (Figure 1 above) and those that don’t (Figure 2 above).  Those who do believe in segments see the world as a multi-modal distribution, a many-humped camel.  Those who don’t see the world as one giant normal distribution, a camel with a single hump.

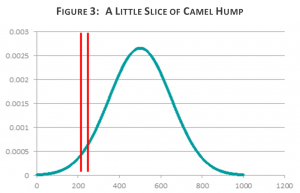Now, if the world was like the first camel, and each hump contained enough people, we could take a sample from each hump and run the single task choice exercise as above, one hump at a time.  But what if the world is like the second camel?  As long as the population is big enough, we can take slices of that single distribution and call them homogeneous segments (Figure 3).  That is what we do now, according to those who believe in the single hump world view, whenever we construct a segmentation model.  We could generate whatever degree of homogeneity we wish simply by slicing smaller and smaller segments.  And then we could conduct our single task choice exercise as above, one slice at a time.

Any population could be deconstructed into these thin slices of camel hump.  For each slice we could estimate utilities and then pool them altogether for the final utility data set.

You might notice that we’ve come to something looking a bit like a Latent Class Choice Model.  A key difference is that we have identified our segments a priori where the LCCM typically uses a dozen or more choice tasks per person to build segments.  Now, we may be able to use LCCM to fine tune our estimates but LCCM is not central to the argument I present here.  Highly homogeneous subgroups of sufficient size.  That’s the mushroom fueling this pipedream.

So if we could somehow identify sufficiently homogeneous segments of sufficient size, we could indeed build disaggregate choice models using just one task per person.  The more heterogeneous the population, the thinner the segment slices would need to be.  But no matter how heterogeneous the population, we could, theoretically, at least, cut our slices thin enough to make them as homogeneous as we want.  And then we could build our single task models.

With online surveying becoming pervasive, sample panels have become enormous, often in the millions of panelists.  So generating sufficient sample size is probably not much of a hurdle, at least not for long.  These same panels often collect a great deal of information on their panelists.  It may soon be possible to identify homogeneous segments (relative to the behavior to be modeled) before the choice exercise is implemented.  Certainly even now, a prior choice study could be used to assign a priori segment membership.

If all this is true, then estimating 30, 40, 50 parameters from a single choice task is not only a possibility, it may also be just around the corner.  Pass me that pipe, will you?